Kernel Trick이란?

• 참고사이트(1): https://sanghyu.tistory.com/14

• 참고사이트(2): https://datascienceschool.net/03%20machine%20learning/13.03%20%EC%BB%A4%EB%84%90%20%EC%84%9C%ED%8F%AC%ED%8A%B8%20%EB%B2%A1%ED%84%B0%20%EB%A8%B8%EC%8B%A0.html

• 아래 그림을 보자, 우리는 1개의 선으로 2개 데이터를 구분할 수 없다

• 그런데 위의 숫자들을 2개의 dimension으로 해보면 어떨까?
• 예를 들어 현재는 $[x_1]$이지만, 이것을 $[x_1, x_1^2]$로 표현해보면 어떨까? 말그대로 1차원에서 2차원으로 옮겨 놓는 것이다.
  • Sample 숫자를 $[-3, -2, -1, 0, 1, 2, 3]$ 이라고 하고, $[-1, 0, 1]$에 해당하는 데이터들이 우리가 구분하려는 데이터라고 해보자.
  • 그렇다면, 이것을 2차원으로 표현하면 아래와 같아질 것이다.
  • $\begin{matrix} -3 & 9 \ -2 & 4 \ -1 & 1 \ 0 & 0 \ 1 & 1 \ 2 & 4 \ 3 & 9 \end{matrix}$
  • 위를 그래프로 표현하면 대략적으로 또 아래와 같은 그림이 될 것이다
  • 
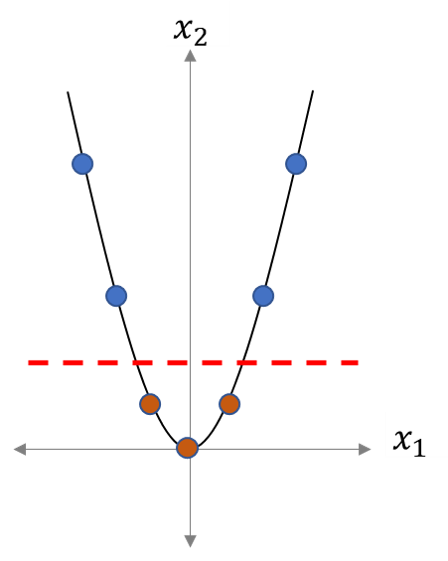
  • 그럼, 우리는 위 그림과 같이 한 개의 선으로 구분할 수 있게 된다.
• 이렇게 저차원에서 고차원으로 mapping하는 식을 바로, mapping function이라 한다.
• 그런데 우리가, 이걸 모델에서 활용한다면 결국, mapping function을 통해 새로운 벡터를 만들고 또 이 벡터끼리 내적을 해야 한다.
  • 여기서 mapping function과 내적 (inner product)을 한번에 하는 것으로
  • 연산 resource를 줄이는 효율적인 방법이 바로, kernel trick이다.